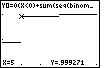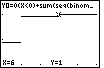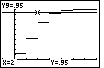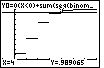Texas-Instruments-Taschenrechner TI- 83

Direkte Berechnung von bgamma-Quantilen einer Binomial-Verteilung
( B(n,p)-Verteilung mit den Parametern n und p (n ... positive ganze Zahl, 0 < p < 1) )

Allgemeine Definition:

Die Kennzahl bgamma, 0 < gamma < 1, einer B(n,p)-verteilten Zufallsgröße X heißt Quantil der Ordnung gamma,
wenn die Ungleichung P( X < bgamma ) < gamma < P( X < bgamma ) erfüllt ist.

Die B(n,p)-verteilte Zufallsgröße X besitzt eine diskrete Verteilungsfunktion F(x) (rechtsseitig stetige Treppenfunktion).
Hat die Gleichung gamma = F(x) keine Lösung,
so ist das gesuchte Quantil bgamma diejenige ganze Zahl x, welche die Ungleichung F(x-0) < gamma < F(x) = F(x+0) erfüllt.

Andernfalls (die Gleichung gamma = F(x) hat (mindestens) eine Lösung) ist bgamma nicht eindeutig bestimmt
und das gesuchte Quantil ist (irgend-)eine Lösung der Gleichung gamma = F(x) mit x aus demjenigen Intervall [k, k+1),
in dem die (kumulative) Verteilungsfunktion F(x) gerade auf dem Wert F(x) = gamma verläuft, oder x=k+1.

Während die direkte Berechnung der zgamma-Quantile einer N(my,sigma2)-Normalverteilung mit dem Funktionsaufruf invNorm(gamma,my,sigma) erfolgen kann (im DISTR-Menü), ist die direkte Berechnung anderer Quantile nicht vorgesehen.

1. Lösungsweg mit der Wertetabelle der Verteilungsfunktion F(x) (LIST)

Aufgabe: Man bestimme das bgamma-Quantil, gamma = 0,95 , einer B( 6; 0,3 ) - Verteilung.


b_quant0.gif
b_quant1.gif

Aufruf des SetUpEditors (Listenfestlegung im STAT-EDIT-Menü) im CATALOG

und Festlegung der Listen L1,L2 

b_quant2.gif

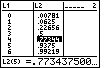
Abspeicherung der x-Werte der Zufallsgröße X (Sprungstellen der Treppenfunktion F(x), hier in x=0(1)6) in Liste L1

Abspeicherung der Funktionswerte von F(x) (Höhe der Treppenstufen = binomcdf(6,.3), d.h. n=6 und p=0,3 gewählt) in Liste L2 

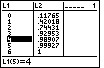
b_quant3.gif

Ansicht der erstellten Listen im STAT-EDIT-Menü:

In der Sprungstelle x=4 wird das gamma-Niveau durch F(x) erstmalig erreicht und sofort überschritten.
Damit ist das gesuchte Quantil die Kennzahl b0,95 = 4 .

2. Graphische Darstellung der Verteilungsfunktion F(x) (GRAPH)

Aufgabe: Man bestimme das bgamma-Quantil, gamma = 0,95 , einer B( 6; 0,3 ) - Verteilung.


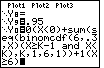
b_quant4.gif
b_quant5.gif
b_quant6.gif

Definition der Verteilungsfunktion Y0=F(x) als rechtsseitig stetige Treppenfunktion im Y= - Fenster:

Y0 = 0 ( X < 0 ) + sum( seq( binomcdf( 6, .3, X ) (X > K-1 and X < K), K, 1, 6, 1) ) + 1 ( X > 6 )

Es ist erkennbar, daß sich die einzelnen Geradenstücken vorteilhaft als Summe definieren lassen,
wobei jeweils nur ein Summand binomcdf( 6, .3, X ) in Abhängigkeit von X
und der Bedingung (X > K-1 and X < K) wirksam wird.


Festlegung des Graphik-Fensters (WINDOW).





Der letzte Sprung bei x=6 auf die Höhe 1 ist wegen der geringen Sprunghöhe nicht erkennbar. 

b_quant7.gif
b_quant8.gif
b_quant9.gif

Bildausschnitt zur Verdeutlichung des letzten Sprungs an der Stelle x=6.

Dazu wurde das Graphik-Fenster neu eingestellt (WINDOW). 

b_quanta.gif
b_quantb.gif
b_quantc.gif
b_quantd.gif

Einstellung des Graphik-Fensters (WINDOW)

Darstellung der Treppenfunktion und der horizontalen Geraden Y9=0,95

Anzeige verschiedener Funktionswerte, um zu erkennen, wo das 0,95-Niveau erreicht und überschritten wird. 

b_quante.gif

Damit ist das gesuchte Quantil die Kennzahl b0,95 = 4 .

3. Beispiel für ein nicht eindeutig bestimmtes Quantil (LIST)

Aufgabe: Man bestimme das bgamma-Quantil, gamma = 0,9375 , einer B( 7; 0,5 ) - Verteilung.

Lösung: Es gilt F(5) = 15/16 = 0,9375 = gamma und folglich erfüllt jede Zahl bgamma mit 5 < bgamma < 6 die oben angegebene allgemeine Definition für ein Quantil der Ordnung gamma. 

b_quantf.gif
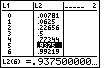
b_quantg.gif
b_quanth.gif

Ansicht der erstellten Listen im STAT-EDIT-Menü:

In der Sprungstelle x=5 wird das gamma-Niveau durch die Verteilungsfunktion F(x) exakt erreicht.

Damit ist das gesuchte Quantil nicht eindeutig bestimmt.

Als Kennzahl b0,9375 kann somit jeder Zahlenwert aus dem Intervall [5; 6] benutzt werden.

Es gilt also z.B.:

0,7734375 = F(5,0-0) < 0,9375 < F(5,0) = F(5,0+0) = 0,9375000 ;

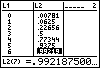
0,9375000 = F(5,3-0) < 0,9375 < F(5,3) = F(5,3+0) = 0,9375000 oder

0,9375000 = F(6,0-0) < 0,9375 < F(6,0) = F(6,0+0) = 0,9921875 .

Programmvarianten für die Statistik-Taschenrechner EL-9600, CFX-9850G PLUS und ClassPad300 PLUS.

Ludwig Paditz, 27. Mai 1998