Bild 1: Ansicht des Untermenüs für Plot1 mit Einstellung auf NormProbPlot | Bild 2: Nutzung des ZoomStat im ZOOM-Menü zur Anpassung des Grafik-Fensters an die darzustellende Punktwolke |
Wir betrachten dazu den Datensatz (Urliste mit n = 60) aus Beispiel 17.1 im Lehr- und Übungsbuch Mathematik, Band 3: Lineare Algebra - Stochastik, S. 232, (von Aulenbacher,G., Paditz,L., Wabel-Frenk,U. (Hrg. v. Prof. Dr .W.Preuß, HTW Dresden(FH), u. Prof. Dr. G.Wenisch, FH Darmstadt), 1. Aufl., Fachbuchverlag Leipzig im Hanser Verl. München 1996):
16 |
15 |
17 |
16 |
19 |
17 |
16 |
16 |
16 |
18 |
15 |
14 |
14 |
14 |
15 |
11 |
7 |
8 |
10 |
9 |
11 |
11 |
13 |
12 |
12 |
12 |
14 |
13 |
13 |
15 |
11 |
9 |
12 |
10 |
12 |
11 |
12 |
14 |
13 |
11 |
12 |
14 |
15 |
13 |
14 |
15 |
18 |
16 |
17 |
16 |
15 |
14 |
13 |
14 |
14 |
12 |
14 |
12 |
13 |
12 |
Die primäre Häufigkeitstabelle hat folgende Gestalt:
Index |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
xi |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
hi |
1 |
1 |
2 |
2 |
6 |
10 |
7 |
11 |
7 |
7 |
3 |
2 |
1 |
hi / n |
1/60 |
1/60 |
2/60 |
2/60 |
6/60 |
10/60 |
7/60 |
11/60 |
7/60 |
7/60 |
3/60 |
2/60 |
1/60 |
sum hi / n |
1/60 |
2/60 |
4/60 |
6/60 |
12/60 |
22/60 |
29/60 |
40/60 |
47/60 |
54/60 |
57/60 |
59/60 |
60/60 |
sum [%] |
1,67 |
3,33 |
6,67 |
10,0 |
20,0 |
36,67 |
48,33 |
66,67 |
78,33 |
90,0 |
95,0 |
98,33 |
100,0 |
Die empirische Verteilungsfunktion y = wn(x) wird dem Lehr- und Übungsbuch Mathematik, Band 3: Lineare Algebra - Stochastik entnommen, vgl. S. 238, Formel (17.15) und Bild 17.2,
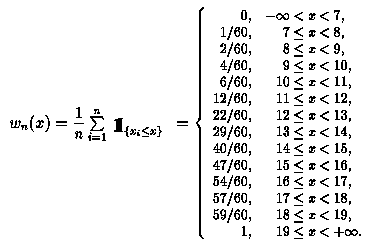
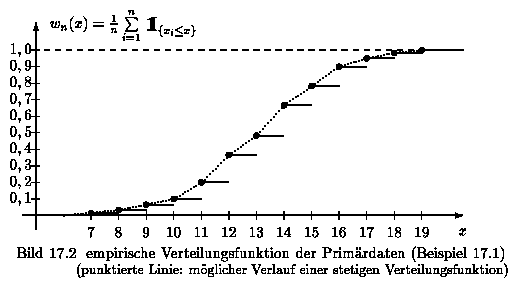
Es folgen nun zwei Darstellungen der empirischen Verteilungsfunktion im Wahrscheinlichkeitspapier:
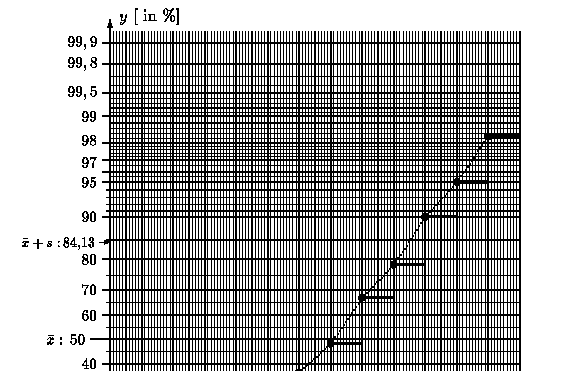
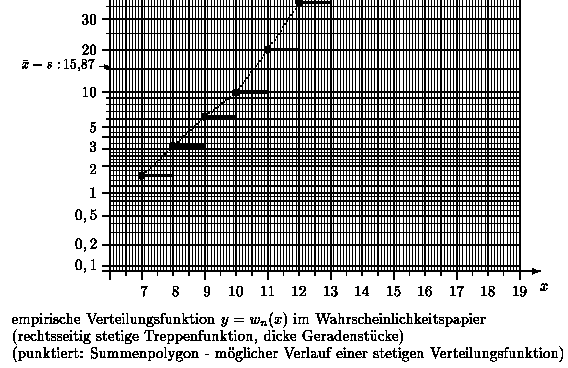

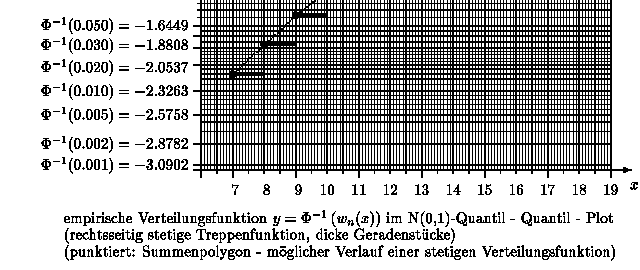
Durch den Übergang vom Wahrscheinlichkeitsniveau gamma zu den entsprechenden Quantilen y = zgamma = Phi-1( gamma) einer Normalverteilung wird die verzerrte Skalierung der y-Achse aufgehoben:
Die x- und y-Achse sind beide ohne Verzerrung skaliert. Die x-Achse enthält die "Quantile" der Urdaten (Variationsreihe) - also die Urdaten selbst. Die y-Achse enthält die "Quantile" einer Normalverteilung. Besitzt die so dargestellte Punktwolke ( x*k , yk ) , k = 1, 2, ..., n-1 , mit x*k = k-te Wert in der Variationsreihe und yk = Phi-1( k / n ) einen linearen Trend, so kann man vermuten, daß die Datenerhebung aus einer normalverteilten Grundgesamtheit herrührte.
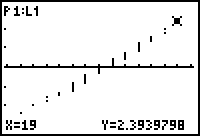
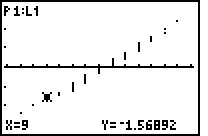
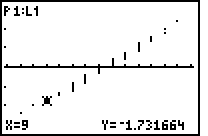
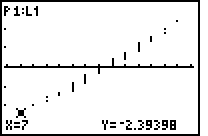
Verschiedene NormProbPlots mit Anzeige einzelner Koordinaten zu Punkten in der Punktwolke im Vergleich zur Darstellung im Wahrscheinlichkeitspapier:
| Bild 3: Der größte Wert der Stichprobe x = 19 ( n-te Wert in der Variationsreihe) erhält nicht wie üblich das Wahrscheinlichkeitsniveau 100% (dann wäre dieser Punkt genau wie im Wahrscheinlichkeitspapier nicht mehr darstellbar), sondern das um ( 1 / 2n ) * 100% reduzierte Wahrscheinlichkeitsniveau (( 2n - 1) / 2n ) * 100% = 98,33% und damit den y-Wert invNorm(119/120) = Phi-1(0,9833) = 2.3939... usw. |
| Bild 4: Der vierte Wert x = 9 in der Variationsreihe der Stichprobe erhält nicht wie üblich das Wahrscheinlichkeitsniveau ( 4 / n ) * 100% = 6,667% , sondern das um ( 1 / 2n ) * 100% reduzierte Wahrscheinlichkeitsniveau ( 7 / 2n ) * 100% = 5,833% und damit den y-Wert invNorm(7/120) = Phi-1(0,05833) = -1,5689... |
| Bild 5: Der dritte Wert x = 9 in der Variationsreihe der Stichprobe erhält nicht wie üblich das Wahrscheinlichkeitsniveau ( 3 / n ) * 100% = 5,000% , sondern das um ( 1 / 2n ) * 100% reduzierte Wahrscheinlichkeitsniveau ( 5 / 2n ) * 100% = 4,167% und damit den y-Wert invNorm(5/120) = Phi-1(0,04167) = -1,7316... |
| Bild 6: Der kleinste Wert der Stichprobe x = 7 erhält nicht wie üblich das Wahrscheinlichkeitsniveau ( 1 / n ) * 100% = 1,67% (dann würde dieser Punkt genau wie im Wahrscheinlichkeitspapier dargestellt), sondern das um ( 1 / 2n ) * 100% reduzierte Wahrscheinlichkeitsniveau ( 1 / 2n ) * 100% = 0,833% und damit den y-Wert invNorm(1/120) = Phi-1(0,0833) = -2.3939... |
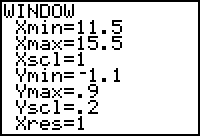
| Bild 7: Notwendige Voreinstellung in WINDOW zur Darstellung eines Bildausschnittes |
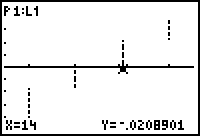
| Bild 8: Bildausschnitt aus dem NormProbPlot: deutlich sichtbar werden die senkrecht übereinanderliegenden Punkte bei Datenhäufung in einem bestimmten x-Wert Cursor hier bei x*30 = 14 und y = invNorm((2*30-1)/120) = -0.02089... |
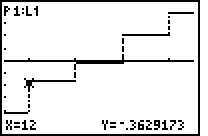
| Bild 9: zusätzliche Darstellung der empirischen Verteilungsfunktion (Treppenfunktion) aus dem Wahrscheinlichkeitspapier: y = ... + invNorm(12/60)(X>11 and X<12) + invNorm(22/60)(X>12 and X<13) + ... . Cursor hier bei x*22 = 12 und y = invNorm((2*22-1)/120) = -0.36291..., d.h. es wird nicht ganz die Höhe der Treppenfunktion erreicht (Erklärung dazu weiter unten). |
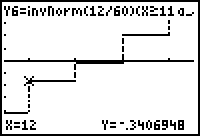
| Bild 10: zusätzliche Darstellung der empirischen Verteilungsfunktion (Treppenfunktion) aus dem Wahrscheinlichkeitspapier: y = ... + invNorm(12/60)(X>11 and X<12) + invNorm(22/60)(X>12 and X<13) + ... . Cursor hier bei x = 12 und y = invNorm(22/60) = -0.34069..., wobei 22/60 der gerade erreichte Wert in der Treppenfunktion ist. |
Allgemein gilt damit für die Darstellung im TI-83 folgender Zusammenhang:
Dem k-ten x-Wert in der Variationsreihe wird das (kumulierte) Wahrscheinlichkeitsniveau (( 2k -1 ) / 2n ) * 100% und damit das N(0,1)-Quantil invNorm( ( 2k -1 ) / 2n ) = Phi-1( ( 2k -1 ) / 2n ) = z( 2k -1 ) / 2n zugeordnet. Damit liegt die Punktwolke im NormProbPlot etwas tiefer als im Wahrscheinlichkeitspapier. Der gewünschte Vergleich mit einer Geraden (Verlauf der Verteilungsfunktion einer Normalverteilung im Wahrscheinlichkeitspapier bzw. im NormProbPlot) wird dadurch nicht beeinträchtigt.Wegen der Nichteindeutigkeit der Quantil-Bestimmung für nicht streng monotone (empirische) Verteilungsfunktionen (rechtsseitig stetige Treppenfunktionen) stehen die Darstellungen im Wahrscheinlichkeitspapier und im NormProbPlot nicht im Widerspruch zueinander !
Der k-te Wert x*k in der Variationsreihe ist nämlich gleichzeitig Quantil der empirischen Verteilungsfunktion sowohl zum Niveau k / n als auch zum Niveau ( 2k - 1 ) / 2n und nicht zuletzt auch zum Niveau k / ( n + 1 ) oder ( k - 1 ) / n usw.
Zur Erinnerung die Quantil-Definition:
Die Kennzahl xgamma, 0 < gamma < 1, einer Zufallsgröße X heißt Quantil der Ordnung gamma,
wenn die Ungleichung P( X < xgamma ) < gamma < P( X < xgamma ) erfüllt ist.
Damit erfüllt der k-te Wert x*k der Variationsreihe die Quantil-Definition sowohl für das Wahrscheinlichkeitsniveau k / n als auch für das Wahrscheinlichkeitsniveau ( 2k - 1 ) / 2n (und auch für das Wahrscheinlichkeitsniveau k / ( n + 1 ) oder ( k - 1 ) / n, also für jedes Niveau gamma mit ( k - 1 ) / n < gamma < k / n ):
P( X < x*k ) < k / n < P( X < x*k ) und P( X < x*k ) = ( k - 1 ) / n < ( 2k - 1 ) / 2n < P( X < x*k ) = k / n
Deshalb ist es korrekt, im Bedienhandbuch davon zu sprechen, daß im NormProbPlot "jedes beobachtete x in der Data List gegen das entsprechende Quantil z der Standardnormalverteilung abgebildet" wird, obwohl im Vergleich zum Wahrscheinlichkeitspapier die Punktwolke etwas niedriger liegt.
-
Ludwig Paditz,
02. August 1999