CASIO-Taschenrechner CFX-9850G PLUS / CFX-9970G

Normalverteilungs-Quantil-Quantil-Plot
(statistische Grafik vom Typ "NPP - Normal Probability Plot")

Das Normalverteilungs-Quantil-Quantil-Plot wird im deutschen Bedienhandbuch zum CFX-9850G PLUS (oder CFX-9970G) auf S. 255 abweichend von den in der Statistik üblichen Begriffen etwas unzutreffend als "normale Wahrscheinlichkeits-Plottgrafik" bezeichnet. Damit bleibt zunächst unklar, welche statistische Grafik sich hinter der "normalen Wahrscheinlichkeits-Plottgrafik" einer konkreten Stichprobe L₁ = { x₁, x₂, ..., x_n } verbirgt.

Im Bedienhandbuch findet man dazu auf S. 255 die nicht dem üblichen Sprachgebrauch in der Statistik entsprechenden Erläuterungen:

"Das Plotten der normalen Wahrscheinlichkeit vergleicht die angesammelte Proportion der Variablen mit der angesammelten Proportion der Normalverteilung und plottet das Ergebnis."
(also: Das Plotten ... vergleicht ... und plottet ... . - Der Schüler soll in der Schule neben Mathematik auch Deutsch lernen. Das Bedienhandbuch wirkt hier diesen Lernzielen offenbar entgegen.)

"Die erwarteten Werte der Normalverteilung werden als vertikale Achse verwendet, wogegen die beobachteten Werte der geprüften Variablen als horizontale Achse verwendet werden."
(also: Die ... Werte ... werden als ... Achse verwendet. - Auch kein gutes Deutsch, Inhalt ohnehin unklar.)

Auf S. 254 des Bedienhandbuches wird die statistische Grafik vom Typ NPP als Normale Wahrscheinlichkeitskurve bezeichnet.

Am besten wird es sein, im englischen Bedienhandbuch nachzuschlagen, um nähere Informationen zur statistischen Grafik vom Typ NPP zu bekommen. Man findet das Handbuch als pdf-File im Internet unter der Adresse http://www.casio.co.jp/edu_e/support/manual/9970g.html oder http://support.casio.com/de/manual/004/CFX-9850GBPLUS_DE.pdf.

Im Kapitel 18-2 des Bedienhandbuches liest man ebenfalls auf S.255 folgende Erklärung:

Es wird hier zumindest der im Englischen übliche Begriff "NPP - Normal Probability Plot" benutzt, aber man hat auch hier das ungute Gefühl, daß die englischen Erläuterungen genau wie im Deutschen nicht den Kern der Sache treffen.

Ein Blick in das englische Bedienhandbuch z.B. des TI-83 PLUS, siehe http://education.ti.com/de/deutschland/products/graphikrechner-und-cas/ti-83-plus/downloads/guidebooks verschafft hier Klarheit:

Zunächst wird eine Interpretation der oben zitierten Erläuterungen aus dem deutschen Bedienhandbuch gegeben:

"Die statistische Grafik vom Typ NPP ist ein Normalverteilungs-Quantil-Quantil-Plot, wobei die konkreten Stichprobenwerte { x₁, x₂, ..., x_n } als Quantile der empirischen Verteilungsfunktion angesehen und den entsprechenden Quantilen der Standard-Normalverteilung zugeordnet werden. Die Zuordnung erfolgt dabei über die um jeweils 1 / 2n reduzierten kumulativen Häufigkeiten der empirischen Verteilungsfunktion."

"Die Quantile { x₁, x₂, ..., x_n } werden als Abszissen auf der x-Achse (horizontalen Achse) und die zugeordneten Quantile der Standard-Normalverteilung als Ordinaten auf der y-Achse (vertikale Achse) dargestellt."

Es wird nun eine konkrete Stichprobe L₁ = { x₁, x₂, ..., x₆₀ } untersucht. Die Festlegungen (SET UP) und Dateneingabe zur oben betrachteten statistischen Grafik vom Typ NPP erfolgen im STAT - Menü z. B. des CFX-9850G PLUS:

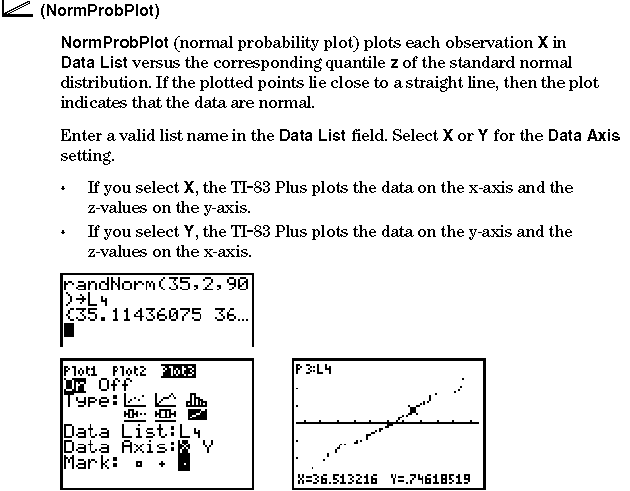
Bild 1:

Aufruf des STAT - Menüs zur Dateneingabe in List 1

Bild 2:

Dateneingabe im List 1 - Arbeitsfenster,
List 1 muß eine Urliste (mit allen Datenwiederholungen) sein.

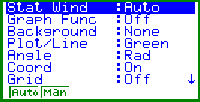
Bild 3:

Aufruf eines weiteren Untermenüs für das SET UP

Einstellung auf automatische Fensteranpassung für die statistische Grafik mit Stat Wind :Auto

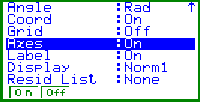
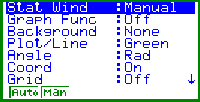
Bild 4:

Weitere Einstellungen im SET UP

speziell muß Coord :On eingestellt sein, um später über die Trace-Taste Punktkoordinaten abfragen zu können.

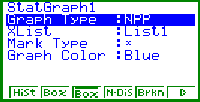
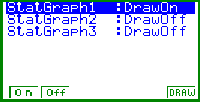
Bild 5:

Einstellungen für die statistische Grafik StatGraph1

Bild 6:

Aktivierung der statistischen Grafik StatGraph1 :On

Bild 7:

Das View Window mit Zoom - Auto ist optimal

(Xscale und Yscale muß per Hand eingetragen werden.)

Bild 8:

Umstellung des Automatic-Zoom auf Stat Wind :Manual, falls der Fensterausschnitt später per Hand eingestellt werden soll.

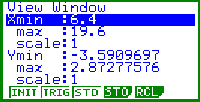
Bild 9:

Das View Window nach der Einstellung per Hand

Die Darstellung der statistischen Grafik NPP wird durch Betätigen der GRPH-, der GPH1- und anschließend der Trace-Taste erhalten und weiter unten abgebildet.

Wir betrachten dazu den Datensatz (Urliste mit n = 60) aus Beispiel 17.1 im Lehr- und Übungsbuch Mathematik, Band 3: Lineare Algebra - Stochastik, S. 232, (von Aulenbacher,G., Paditz,L., Wabel-Frenk,U. (Hrg. v. Prof. Dr .W.Preuß, HTW Dresden, u. Prof. Dr. G.Wenisch, FH Darmstadt), 2. Aufl., Fachbuchverlag Leipzig im Hanser Verl. München, 2.Aufl. 2001):

16	15	17	16	19	17	16	16	16	18	15	14	14	14	15
11	7	8	10	9	11	11	13	12	12	12	14	13	13	15
11	9	12	10	12	11	12	14	13	11	12	14	15	13	14
15	18	16	17	16	15	14	13	14	14	12	14	12	13	12

Die primäre Häufigkeitstabelle hat folgende Gestalt:

Index	1	2	3	4	5	6	7	8	9	10	11	12	13
x_i	7	8	9	10	11	12	13	14	15	16	17	18	19
h_i	1	1	2	2	6	10	7	11	7	7	3	2	1
h_i / n	1/60	1/60	2/60	2/60	6/60	10/60	7/60	11/60	7/60	7/60	3/60	2/60	1/60
sum h_i / n	1/60	2/60	4/60	6/60	12/60	22/60	29/60	40/60	47/60	54/60	57/60	59/60	60/60
sum [%]	1,67	3,33	6,67	10,0	20,0	36,67	48,33	66,67	78,33	90,0	95,0	98,33	100,0

Die empirische Verteilungsfunktion y = w_n(x) wird dem Lehr- und Übungsbuch Mathematik, Band 3: Lineare Algebra - Stochastik entnommen, vgl. S. 238, Formel (17.15) und Bild 17.2,

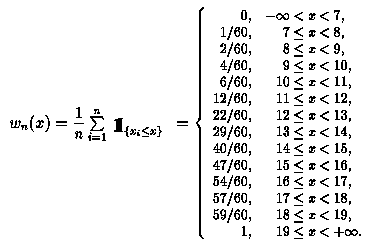
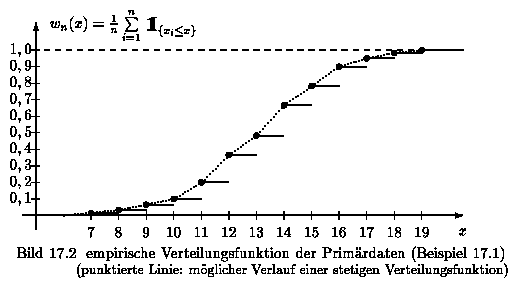
Es folgen nun zwei Darstellungen der empirischen Verteilungsfunktion im Wahrscheinlichkeitspapier:

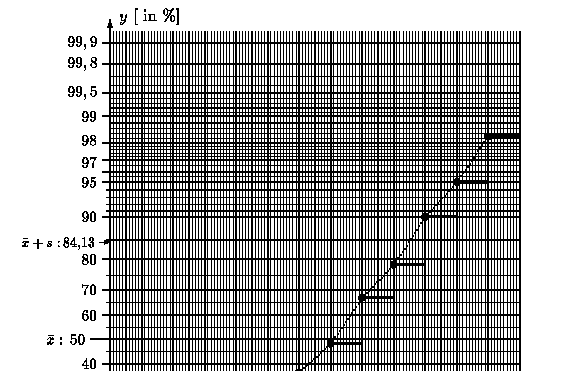
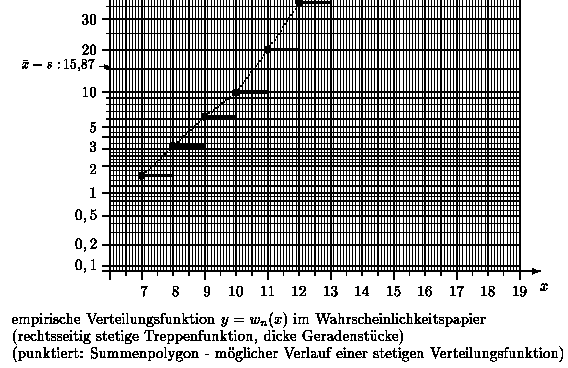
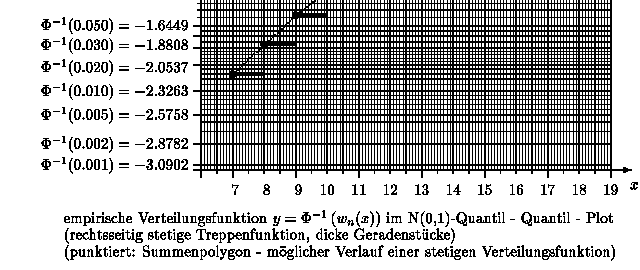
Durch den Übergang vom Wahrscheinlichkeitsniveau gamma zu den entsprechenden Quantilen y = z_gamma = Phi^-1( gamma) einer Normalverteilung wird die verzerrte Skalierung der y-Achse aufgehoben:

Die x- und y-Achse sind beide ohne Verzerrung skaliert. Die x-Achse enthält die "Quantile" der Urdaten (Variationsreihe) - also die Urdaten selbst. Die y-Achse enthält die "Quantile" einer Normalverteilung. Besitzt die so dargestellte Punktwolke ( x^*_k , y_k ) , k = 1, 2, ..., n-1 , mit x^*_k = k-te Wert in der Variationsreihe und y_k = Phi^-1( k / n ) einen linearen Trend, so kann man vermuten, daß die Datenerhebung aus einer normalverteilten Grundgesamtheit herrührte.

Verschiedene statistische Grafiken vom Typ NPP mit Anzeige einzelner Koordinaten zu Punkten in der Punktwolke im Vergleich zur Darstellung im Wahrscheinlichkeitspapier:

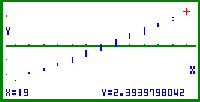
Bild 10:

Der größte Wert der Stichprobe x = 19 ( n-te Wert in der Variationsreihe, s. Cursor) erhält nicht wie üblich das Wahrscheinlichkeitsniveau 100%
(dann wäre dieser Punkt genau wie im Wahrscheinlichkeitspapier nicht mehr darstellbar),

sondern das um ( 1 / 2n ) * 100% reduzierte Wahrscheinlichkeitsniveau

(( 2n - 1) / 2n ) * 100% = 98,33% und damit den y-Wert

InvN(119/120) = Phi^-1(0,9833) = 2.3939...

usw.

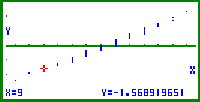
Bild 11:

Der vierte Wert x = 9 in der Variationsreihe der Stichprobe (s. Cursor) erhält nicht wie üblich das Wahrscheinlichkeitsniveau ( 4 / n ) * 100% = 6,667% ,

sondern das um ( 1 / 2n ) * 100% reduzierte Wahrscheinlichkeitsniveau

( 7 / 2n ) * 100% = 5,833% und damit den y-Wert

InvN(7/120) = Phi^-1(0,05833) = -1,5689...

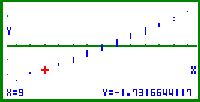
Bild 12:

Der dritte Wert x = 9 in der Variationsreihe der Stichprobe (s. Cursor) erhält nicht wie üblich das Wahrscheinlichkeitsniveau ( 3 / n ) * 100% = 5,000% ,

sondern das um ( 1 / 2n ) * 100% reduzierte Wahrscheinlichkeitsniveau

( 5 / 2n ) * 100% = 4,167% und damit den y-Wert

InvN(5/120) = Phi^-1(0,04167) = -1,7316...

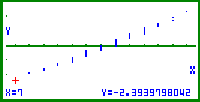
Bild 13:

Der kleinste Wert der Stichprobe x = 7 (s. Cursor) erhält nicht wie üblich das
Wahrscheinlichkeitsniveau ( 1 / n ) * 100% = 1,67%
(dann würde dieser Punkt genau wie im Wahrscheinlichkeitspapier dargestellt),

sondern das um ( 1 / 2n ) * 100% reduzierte Wahrscheinlichkeitsniveau

( 1 / 2n ) * 100% = 0,833% und damit den y-Wert

InvN(1/120) = Phi^-1(0,0833) = -2.3939...

Bild 14:

Notwendige Voreinstellung in View Window zur Darstellung eines Bildausschnittes

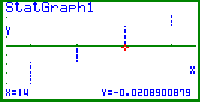
Bild 15:

Bildausschnitt aus der statistischen Grafik NPP:
deutlich sichtbar werden die senkrecht übereinanderliegenden Punkte bei Datenhäufung in einem bestimmten x-Wert

Der Cursor zeigt hier bei x^*₃₀ = 14 auf den untersten Punkt bei

y = InvN((2*30-1)/120) = -0,02089...

Bild 16:
Programmierung der empirischen Verteilungsfunktion y = w_n(x) (Treppenfunktion)
mit Hilfe von Rechteckimpulsen f₁ bis f₅, s. Bild 17.
hier Eingabe von f₁ im RUN-Modus:

f₁ = ( 50 * | x-10.99 | - 50 * | x-11 | - 50 * | x-12 | + 50 * | x-12.01 | ) (für Rechteckimpuls der Höhe 1 über 11 < x < 12 )

usw.

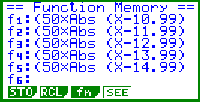
Bild 17:

Darstellung der Rechteckimpulse f₁ bis f₅ im Function Memory zum weiteren Abruf im Y = - Fenster, vgl. Bild 18.

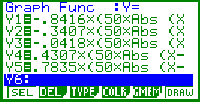
Bild 18:

Skalierung der Rechteckimpulse auf die erforderlichen Höhen im NormProbPlot:

z.B. Y1 = -0,8416 * f₁ = InvN(12/60) * f₁ usw.

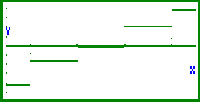
Bild 19:

Bildfenster der Funktions-Grafik:

Darstellung der empirischen Verteilungsfunktion (Treppenfunktion) aus dem Wahrscheinlichkeitspapier durch Überlagerung der Rechteckimpulse Y1 bis Y5
(Abspeicherung als Background - Picture für die statistische Grafik NPP)

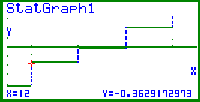
Bild 20:
Bildfenster der statistischen Grafik NPP:
Überlagerung des NormProbPlots und der empirischen Verteilungsfunktion (Treppenfunktion) aus dem Wahrscheinlichkeitspapier.
(Im SET UP für StatGraph1 wurde die Treppenfunktion als Background deklariert, da sich unterschiedliche Grafik-Typen (Funktionsgrafik und statistische Grafik) nicht gleichzeitig zeichnen lassen.)
Der Cursor steht auf dem Wert x^*₂₂ =12 mit dem Quantil-Niveau 43/120 und
InvN( 43 / 120 ) = -0,3629... < InvN( 22 / 60 ) = -0,34069...
( InvN( 22 / 60 ) als Wert der Treppenfunktion für 12 < x < 13 ),
d.h. die Punktwolke im NormProbPlot ist um das Niveau 1 / n = 1 / 120 nach unten verschoben.

Bemerkung: Der grüne Rahmen wurde nachträglich um die Bilder gezeichnet.

Hinweis: Link zum NormProbPlot mit dem TI-83 oder mit dem EL-9600,
wobei sowohl beim TI-83 (s. dort Bild 9 und Bild 10: bedingte Funktionswertbefehle im Y = - Menü möglich!)
als auch beim EL-9600 (s. dort Bild 13 u. 14: Line-Befehle im Draw-Menü!)
unterschiedliche Programmierungsmöglichkeiten für die Treppenfunktion genutzt wurden, die teilweise nur auf dem speziellen Taschenrechnermodell programmierbar sind.

Allgemein gilt damit für die Darstellung im CFX-9850G PLUS / CFX-9970G folgender Zusammenhang:

Dem k-ten x-Wert in der Variationsreihe wird das (kumulierte) Wahrscheinlichkeitsniveau (( 2k -1 ) / 2n ) * 100% und damit das N(0,1)-Quantil InvNorm( ( 2k -1 ) / 2n ) = Phi^-1( ( 2k -1 ) / 2n ) = z_{( 2k -1 ) / 2n} zugeordnet. Damit liegt die Punktwolke im NormProbPlot etwas tiefer als im Wahrscheinlichkeitspapier. Der gewünschte Vergleich mit einer Geraden (Verlauf der Verteilungsfunktion einer Normalverteilung im Wahrscheinlichkeitspapier bzw. im NormProbPlot) wird dadurch nicht beeinträchtigt.

Wegen der Nichteindeutigkeit der Quantil-Bestimmung für nicht streng monotone (empirische) Verteilungsfunktionen (rechtsseitig stetige Treppenfunktionen) stehen die Darstellungen im Wahrscheinlichkeitspapier und im NormProbPlot nicht im Widerspruch zueinander !
Der k-te Wert x^*_k in der Variationsreihe ist nämlich gleichzeitig Quantil der empirischen Verteilungsfunktion sowohl zum Niveau k / n als auch zum Niveau ( 2k - 1 ) / 2n und nicht zuletzt auch zum Niveau k / ( n + 1 ) oder ( k - 1 ) / n usw.

Zur Erinnerung die Quantil-Definition:

Die Kennzahl x_gamma, 0 < gamma < 1, einer Zufallsgröße X heißt Quantil der Ordnung gamma,
wenn die Ungleichung P( X < x_gamma ) < gamma < P( X < x_gamma ) erfüllt ist.

Damit erfüllt der k-te Wert x^*_k der Variationsreihe die Quantil-Definition sowohl für das Wahrscheinlichkeitsniveau k / n als auch für das Wahrscheinlichkeitsniveau ( 2k - 1 ) / 2n (und auch für das Wahrscheinlichkeitsniveau k / ( n + 1 ) oder ( k - 1 ) / n, also für jedes Niveau gamma mit ( k - 1 ) / n < gamma < k / n ):

P( X < x^*_k ) < k / n < P( X < x^*_k ) und P( X < x^*_k ) = ( k - 1 ) / n < ( 2k - 1 ) / 2n < P( X < x^*_k ) = k / n

Damit ist die statistische Grafik vom Typ NPP korrekt, obwohl im Vergleich zum Wahrscheinlichkeitspapier die Punktwolke etwas niedriger liegt.

Ludwig Paditz, 15. März 2000

16	15	17	16	19	17	16	16	16	18	15	14	14	14	15
11	7	8	10	9	11	11	13	12	12	12	14	13	13	15
11	9	12	10	12	11	12	14	13	11	12	14	15	13	14
15	18	16	17	16	15	14	13	14	14	12	14	12	13	12

16	15	17	16	19	17	16	16	16	18	15	14	14	14	15
11	7	8	10	9	11	11	13	12	12	12	14	13	13	15
11	9	12	10	12	11	12	14	13	11	12	14	15	13	14
15	18	16	17	16	15	14	13	14	14	12	14	12	13	12

CASIO-Taschenrechner CFX-9850G PLUS / CFX-9970G

Normalverteilungs-Quantil-Quantil-Plot (statistische Grafik vom Typ "NPP - Normal Probability Plot")

Es folgen nun zwei Darstellungen der empirischen Verteilungsfunktion im Wahrscheinlichkeitspapier:

Verschiedene statistische Grafiken vom Typ NPP mit Anzeige einzelner Koordinaten zu Punkten in der Punktwolke im Vergleich zur Darstellung im Wahrscheinlichkeitspapier:

Allgemein gilt damit für die Darstellung im CFX-9850G PLUS / CFX-9970G folgender Zusammenhang:

Normalverteilungs-Quantil-Quantil-Plot
(statistische Grafik vom Typ "NPP - Normal Probability Plot")

16	15	17	16	19	17	16	16	16	18	15	14	14	14	15
11	7	8	10	9	11	11	13	12	12	12	14	13	13	15
11	9	12	10	12	11	12	14	13	11	12	14	15	13	14
15	18	16	17	16	15	14	13	14	14	12	14	12	13	12