 Bild 1
Bild 1 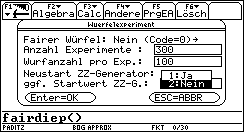 Bild 2
Bild 2
(Eine ausführliche Variante finden Sie hier.)
Welche (Prüf-)Verteilung hat die Testgröße, wenn der Würfel in Wirklichkeit "gezinkt" war?
Wie sind die Wahrscheinlichkeiten für den Fehler 1. und 2. Art zu interpretieren?
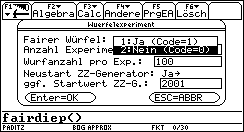
Der Start der Datensimulation erfolgt unter der deutschen Bedienoberfläche mit dem Teilprogramm fairdiep( ) ohne Parametereingabe, denn es wird sofort ein Dialogfenster zur Eingabe der Startwerte geöffnet:
 Bild 1
Bild 1  Bild 2
Bild 2
Die Bilder 1 und 2 zeigen die Auswahlmöglichkeiten. Der Neustart der Zufallszahlengenerators erlaubt es, bereits simulierte Daten erneut zu erzeugen, damit z.B. alle Workshopteilnehmer auf ihren persönlichen Taschenrechnern mit den gleichen Daten arbeiten können. Im ersten Durchlauf werden M=300 Würfelexperimente mit je N=100 Würfen eines idealen Würfels simuliert (Startwert des ZZ-Generators: 2001):
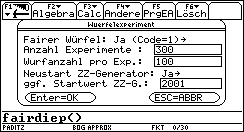 Bild 3
Bild 3 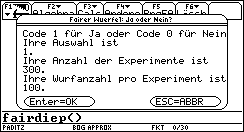 Bild 4
Bild 4
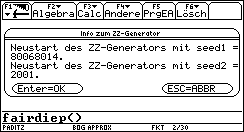 Bild 5
Bild 5 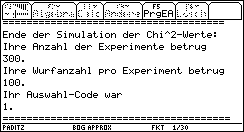 Bild 6
Bild 6
Zeitdauer dieser Simulation ca. 30min (ein Speed-Modul im Ti-92Plus ist vorteilhaft, um die Zeitdauer für die Simulation zu verkürzen). Während die Simulation läuft, können weitere Erläuterungen gegeben werden. Liste list1 mit den M=300 simulierten Chi^2-Werten muß dann in Liste laltur (alte Urdatenliste des ersten Simulationslaufes) gesichert werden. Nun kann die Simulation mit dem gezinkten Würfel erfolgen:
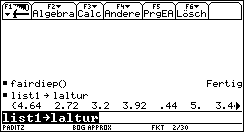 Bild 7
Bild 7 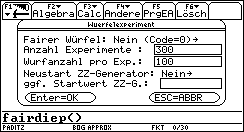 Bild 8
Bild 8
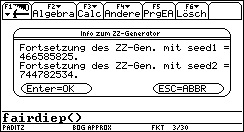 Bild 9
Bild 9 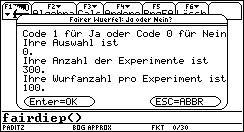 Bild 10
Bild 10
Während des Simulationslaufes erscheint eine Anzeige zum Stand der Simulation. Hier der 9. Chi^2-Wert:
 Bild 11
Bild 11 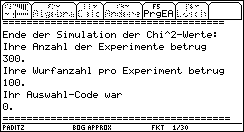 Bild 12
Bild 12
Zeitdauer dieser erneuten Simulation ca. 30min. Während die Simulation läuft, können weitere Erläuterungen gegeben werden. Liste list1 mit den M=300 simulierten Chi^2-Werten muß dann in Liste lneuur (neue Urdatenliste des zweiten Simulationslaufes) gesichert werden.
Diese zwei Urdatenlisten könnten auch vorher von jeden Schüler individuell erzeugt bzw. vom Lehrer überspielt werden, um die Simulationszeit einzusparen.
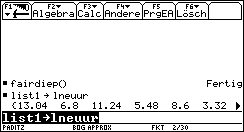 Bild 13
Bild 13 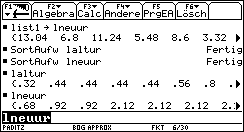 Bild 14
Bild 14
Nun beginnt der nächste Arbeitsschritt:
Erzeugung der Variationsreihen zu laltur und lneuur mit dem SortAufw-Befehl. Die in aufsteigender Reihenfolge sortierten Listen sind wieder unter den bisherigen Listennamen abgespeichert, vgl. Bild 14. Man erkennt bereits die unterschiedlichen Größenordnungen der Einzelwerte in den sortierten Urlisten. Nun werden die primären und sekundären Häufigkeitsverteilungen mit den Teilprogrammen primfreq( ) und secufreq( ) erzeugt und unter folgenden Namen abgespeichert:
 Bild 15
Bild 15 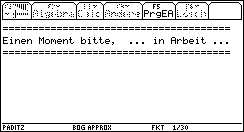 Bild 16
Bild 16
list2 --> laltpx (ältere erste Simulation mit den primären x-Werten)
list3 --> laltpf (ältere erste Simulation mit den primären f-Werten: zugeordnete Häufigkeiten)
list4 --> laltsx (ältere erste Simulation mit den sekundären x-Werten bei Klasseneinteilung: Klassenbreite 1)
list5 --> laltsf (ältere erste Simulation mit den sekundären f-Werten: zugeordnete Klassenhäufigkeiten)
und
list2 --> lneupx (neuere zweite Simulation mit den primären x-Werten)
list3 --> lneupf (neuere zweite Simulation mit den primären f-Werten: zugeordnete Häufigkeiten)
list4 --> lneusx (neuere zweite Simulation mit den sekundären x-Werten bei Klasseneinteilung: Klassenbreite 1)
list5 --> lneusf (neuere zweite Simulation mit den sekundären f-Werten: zugeordnete Klassenhäufigkeiten)
 Bild 17
Bild 17 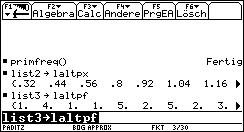 Bild 18
Bild 18
 Bild 19
Bild 19  Bild 20
Bild 20
Nun werden die Häufigkeitsverteilungen für die "gezinkten" Daten bereitgestellt:
 Bild 21
Bild 21  Bild 22
Bild 22
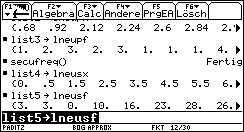 Bild 23
Bild 23 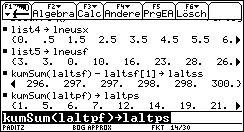 Bild 24
Bild 24
In Bild 24 wurden die Summenhäufigkeiten (Absolutwerte in Liste laltps bzw. laltss) zur Bereitstellung der empirischen Verteilungsfunktion bzw. Treppenfunktion der relativen Summenhäufigkeiten erzeugt. Nun werden außerdem die Chi^2-Dichtefunktion, deren Verteilungsfunktion, die empirische Verteilungsfunktion und die Treppenfunktion der relativen Summenhäufigkeiten definiert und im Y= - Menü abgespeichert, jeweils für den idealen Würfel: defchidf( ) erzeugt y3, defchivf( ) erzeugt y2, defempvf( ) erzeugt y1, deftrels( ) erzeugt y4.
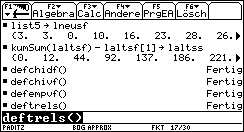 Bild 25
Bild 25 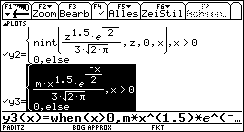 Bild 26
Bild 26
 Bild 27
Bild 27  Bild 28
Bild 28
Das Betrachtungsfenster muß per Hand eingestellt werden. Das Teilprogramm plot1234( ) erzeugt nun einige statistische Grafiken, die teilweise mit der Chi^2-Dichtefunktion überlagert werden:
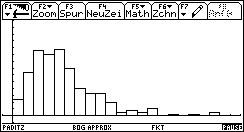 Bild 29
Bild 29 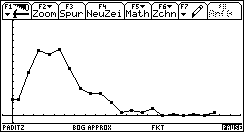 Bild 30
Bild 30
Bild 29 und 30: Histogramm und Häufigkeitspolygon für den idealen Würfel
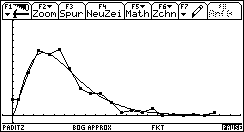 Bild 31
Bild 31 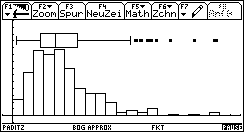 Bild 32
Bild 32
Bild 31 und 32: Häufigkeitspolygon und Chi^2-Dichtefunktion für den idealen Würfel, sowie ein Boxplot.
Konzentration der Chi^2-Werte unter der Nullhypothese H0 "nahe bei Null" - also: kein Einwand gegen H0 .
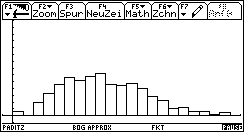 Bild 33
Bild 33 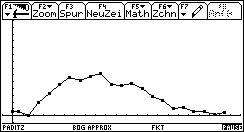 Bild 34
Bild 34
Bild 33 und 34: Histogramm und Häufigkeitspolygon für den "gezinkten" Würfel - Eine Chi^2-Dichtefunktion ist nicht mehr erkennbar (Rechtsverschiebung des Histogramms deutet auf zu große Chi^2-Werte unter H0 hin).
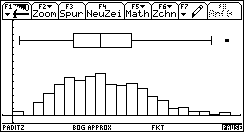 Bild 35:
Histogramm und Boxplot für den gezinkten Würfel.
Bild 35:
Histogramm und Boxplot für den gezinkten Würfel.
Es folgen nun Bilder, die per Hand im Y= - Menü eingestellt werden:
Bild 37 und 39: empirische Verteilungsfunktion (der Chi^2-Testwerte unter H0 und idealem Würfel)
Bild 41: Verteilungsfunktion der Prüfverteilung (Chi^2-Verteilung mit 5 Freiheitsgraden)
Wegen der langen Rechenzeit zur Darstellung der Chi^2-Verteilungsfunktion über ein Integral mit variabler oberer Grenze nutzt man vorteilhaft die Bereitstellung der Funktion über die Statistik-Flash-Software:
y5 = tistat.chi2iwkt(-oo, x, 5) (iwkt = Intervallwahrscheinlichkeit)
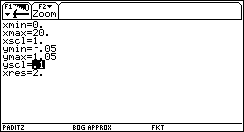 Bild 36
Bild 36 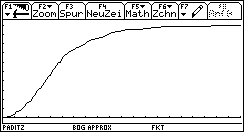 Bild 37
Bild 37
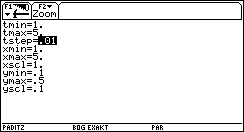 Bild 38
Bild 38 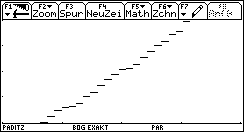 Bild 39
Bild 39
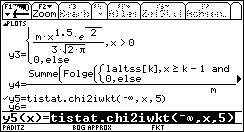 Bild 40
Bild 40 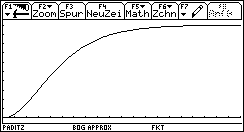 Bild 41
Bild 41
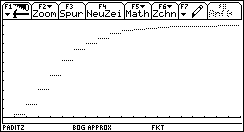 Bild 42
Bild 42 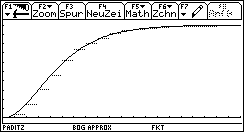 Bild 43
Bild 43
Bild 42 und 43: Treppenfunktion der relativen Summenhäufigkeiten (nach der Klassenbildung) und Chi^2-Verteilungsfunktion. Die Treppenfunktion wurde im "Dot"-Modus gezeichnet, um senkrechte Kurvenstücke zu vermeiden und die Unstetigkeitsstellen deutlich sichtbar zu machen.
Eine bessere Bildqualität erhält man über die Parameterdarstellung (ebenfalls im "Dot"-Modus):
xt1(t) = t und yt1(t) = y4(t) , wenn die Schrittweite hinreichend klein gewählt wird (vgl. auch Bild 38 und 39):
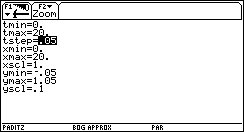 Bild 44
Bild 44 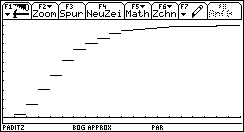 Bild 45
Bild 45
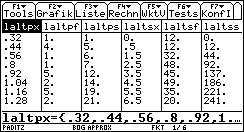 Bild 46
Bild 46 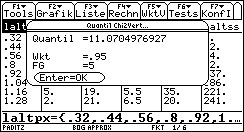 Bild 47
Bild 47
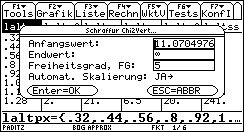 Bild 48
Bild 48 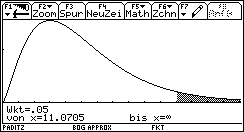 Bild 49
Bild 49
Bild 46 zeigt den Statistik-Listen-Editor und die Auswahlmenüs: F5: Wahrscheinlichkeitsverteilungen/Quantile
Zur Wahrscheinlichkeit alpha = 0,05 für den Fehler erster Art: Im Würfelexperiment können auch für den idealen Würfel Chi^2-Testwerte über 11,0705 entstehen und zwar in 5% der Fälle. Dort würde man auf einem Signifikanz-niveau von alpha = 5% die Nullhypothese ablehnen, obwohl mit einem idealen Würfel gewürfelt wurde.
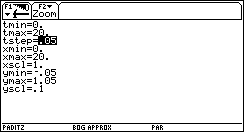 Bild 50
Bild 50 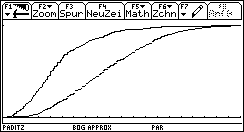 Bild 51
Bild 51
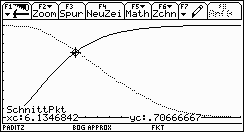 Bild 52
Bild 52 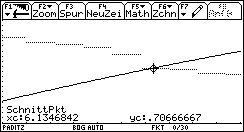 Bild 53
Bild 53
Für die hier betrachteten Hypothesen H0 und HA konnte durch Simulation gezeigt werden, dass in der Tat unter H0 eine Chi^2-verteilte Prüfgröße (5 Freiheitsgrade) entsteht, vgl. Bilder 37, 41 und 43. Hingegen beim "gezinkten" Würfel (unter HA ) zeigten sich deutliche Abweichungen von der ursprünglichen Prüfverteilung, wenn die Prüfgröße weiterhin mit der theoretischen Annahme einer Gleichverteilung berechnet wurde, vgl. Bild 51 mit der Verteilungsfunktion der Prüfverteilung (Chi^2-Verteilung) und der empirischen Verteilungsfunktion der Testwerte für den "gezinkten" Würfel.
In den letzten zwei Bildern wird derjenige Testwert xA = 6,135 berechnet, für den die Wahrscheinlichkeiten alpha = 0,293 und beta = 0,293 der Fehler 1. und 2. Art übereinstimmen. Dazu wurden die Chi^2-Verteilungsfunktion und die Differenzfunktion 1- P( XA< x ) = P( XA > x ) zum Schnitt gebracht.
Damit gilt für die untersuchten Simulationen:
Fällt die Prüfgröße X kleiner als xA = 6,135 aus, dann ist die Wahrscheinlichkeit für den Fehler 1. Art größer als die Wahrscheinlichkeit für den Fehler 2. Art und man sollte die Nullhypothese nicht ablehnen.
Ergibt sich jedoch mit den Würfeldaten (ein Würfelexperiment mit N Würfen) eine Prüfgröße X größer als xA = 6,135, dann ist die Wahrscheinlichkeit für den Fehler 2. Art größer als die Wahrscheinlichkeit für den Fehler 1. Art und man sollte die Nullhypothese besser ablehnen und davon ausgehen, dass der Würfel "gezinkt" ist.
Zur Erinnerung:
Fehler 1. Art: Ablehnung der Nullhypothese, obwohl sie richtig ist.
Fehler 2. Art: Nichtablehnung der Nullhypothese, obwohl die Alternativhypothese richtig ist.
Wegen der langen Rechenzeiten zur Erstellung der Graphen
im Parameter-Modus können die Bilder vorzeitig beendet werden (Abbruch
der Erstellung der Graphik mit der ON-Taste). Der Schnittpunkt der beiden
Graphen wird im Funktions-Modus ermittelt.
Literaturhinweis:
Aulenbacher, Paditz, Wabel-Frenk:Lehr-
und Übungsbuch Mathematik
Bd.3
(Teil Stochastik: Beispiel 6.1 und Aufgabe
19.1),
Fachbuchverlag Leipzig 2001 (2.Aufl.) ( ISBN
3-446-21682-0 )
Programmidee:
C.C.Edwards: Does a TI-8x Cast a Fair Die? in: Eightysomething!,
Vol. 6, No.3, 1997, p. 9-10.
siehe Internet: http://www.comcal.net/www.ti.com/calc/docs/act83stat.htm
oder als PDF-File.
Die oben angeführten Programme sind aus
dem Internet abrufbar:
fairdiep() primfreq() secufreq() defempvf() defempfk() defchivf() defchidf() deftrels() plot1234() |
unter unter unter unter unter unter unter unter unter |
fairdiep.9xp (Simulation der Urdatenlisten) primfreq.9xp (Primäre Häufigkeitsverteilung) secufreq.9xp (Sekundäre Häufigkeitsverteilung) defempvf.9xp (Empirische Vert.-fkt. - 1. Simulation) defempfk.9xp (Empirische Vert.-fkt. - 2. Simulation) defchivf.9xp (Chi^2-Verteilungsfunktion) defchidf.9xp (Chi^2-Dichtefunktion) deftrels.9xp (Treppenfkt. der rel. Summenhäufigkeiten) plot1234.9xp (Definition und Darstellung von Plots) |
bzw. bzw. bzw. bzw. bzw. bzw. bzw. bzw. bzw. |
FAIRDIEP.TXT PRIMFREQ.TXT SECUFREQ.TXT DEFEMPVF.TXT DEFEMPFK.TXT DEFCHIVF.TXT DEFCHIDF.TXT DEFTRELS.TXT PLOT1234.TXT |